-
News
News
Home-News-details
橫向振動作用下螺紋聯接松動過程的實驗研究
2022-12-30
螺紋聯接在聯接件間產生夾緊力,具有結構簡單、拆卸方便、工作可靠等優點,因而廣泛應用于各種機械零部件的聯接。螺紋聯接在振動載荷下工作時,易發生松動,導致預緊力的降低甚至聯接的失效[1]。振動載荷按照其作用方向可分為4類:沿螺栓軸向的拉壓力、垂直于螺栓軸向的剪切力(橫向載荷)、 沿螺栓軸向的扭矩以及垂直于螺栓軸向的扭矩。Junker[2]的研究表明,相對于其他3類振動載荷,橫向振動載荷對螺紋聯接的松動影響最大。橫向振動作用下螺紋聯接的松動過程伴隨著螺母與螺桿沿擰松方向的相對轉動。現有的研究針對橫向振動如何引起螺母與螺桿之間的相對轉動這個問題主要提出了3種解釋:
1) 根據螺紋聯接的滑塊-斜坡模型[3],在同樣的夾緊力作用下,擰緊螺母所需要的力矩大于擰松螺母所需要的力矩。不少學者[4,?5,?6,?7]認為該力矩差的存在是螺紋聯接在振動載荷作用下松動的原因。
2) Junker[2]最早提出螺紋聯接受橫向振動作用時,其周向(擰松方向)的摩擦系數會變小,從而失去自鎖功能,發生滑移并松動。Sakai[8]通過理論計算表明,橫向振動作用下螺紋聯接接觸面間發生周向滑移時其摩擦系數約為0.03,而在不受橫向振動作用時其摩擦系數約為0.15。
3) 橫向振動作用下螺母與螺桿之間的相對轉動是摩擦副的塑性變形造成的[9,?10,?11,?12]。Haviland[13]進一步指出,材料的棘輪效應是引起橫向振動作用下螺紋聯接松動的原因。棘輪效應是指在循環應力加載條件下塑性應變的循環累積現象[14]。
振動載荷作用下螺紋聯接的松動是一個多階段的復雜過程,現有研究對其機理的認識仍然不夠深入。目前,較少有研究定量地描述夾緊力的衰減過程,也鮮有學者對夾緊力在單個振動周期內的變化進行研究。本研究改造了Junker橫向振動試驗機,以改造后的試驗機為實驗平臺研究了橫向振動作用下螺紋聯接夾緊力衰減的過程,并研究了單個振動周期內夾緊力與橫向振動位移的同步變化關系。通過對夾緊力衰減曲線的數值擬合分析,本研究提出了描述夾緊力衰減過程的模型函數,并結合該模型函數分析了橫向振動作用下螺紋聯接松動的機理。
1 實驗概況
????Junker橫向振動試驗機能模擬螺紋聯接在橫向交變載荷作用下的松動過程[15]。圖1是在 Junker 橫向振動試驗機上進行螺紋聯接松動實驗的示意圖。如圖1所示,螺紋聯接的下連接板固定,上下連接板之間通過滾針軸承連接。實驗開始前擰緊螺母,使得螺母與螺栓頭之間夾緊,該夾緊力在數值上等于螺桿所受軸向力。夾緊力通過安裝在螺栓頭與下連接板之間的壓力傳感器測量得到。實驗中,由具有調速機構的電動機驅動可調偏心距的連桿產生橫向往復運動(振動),并通過橫向傳遞裝置將往復運動傳遞至上連接板。由于上連接板相對于下連接板的運動只需克服很小的滾動摩擦力,因而上連接板的橫向振動阻力主要來自于螺母與上連接板之間的剪切力以及螺桿的彎曲變形力。實驗過程中記錄夾緊力的變化。夾緊力的衰減曲線反映了螺紋聯接的松動過程。
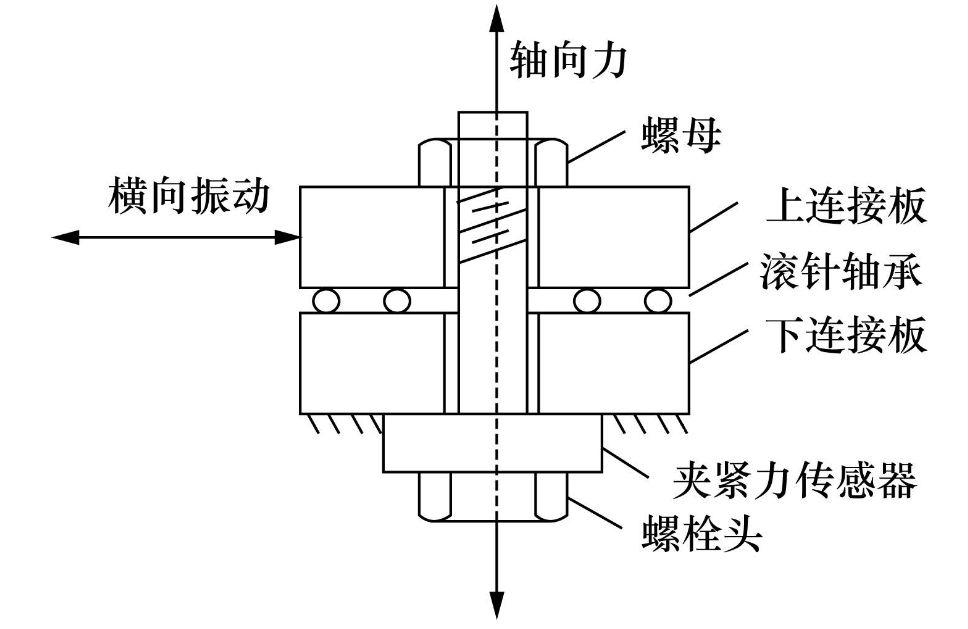
為了精確測量單個振動周期內夾緊力的變化,對Junker橫向振動試驗機進行了如下的改造:1) 增加了圖1中上連接板橫向位移的測量。橫向位移采用電渦流位移傳感器測量。2) 實現了橫向振動過程中螺紋聯接夾緊力與橫向位移之間的同步測量。夾緊力與橫向位移均由數據采集卡NI USB-6251采集,采樣頻率為1 kHz。
橫向振動實驗依據GB/T 10431-2008 緊固件橫向振動實驗方法進行。螺栓與螺母樣品分別為同批次的M16×110-8.8 粗牙六角頭螺栓與M16-10粗牙六角螺母,不使用墊片。實驗前將螺母及螺栓在丙酮溶液中超聲波清洗30 min,以除去螺紋及螺栓表面的油脂。
實驗參數設置如下:橫向振動的頻率為12.5 Hz;振幅分別為0.4、 0.8、 1.2、 1.6、 2.0 mm;對每一個振幅值,進行預緊力(即初始夾緊力)分別為50、 40、 30、 20 kN的松動實驗。預緊力的選擇依據如下:國標緊固件的扭矩-夾緊力試驗標準(GB/T 16823.3—2010)規定,為了防止螺紋聯接整體的塑性變形,試驗力不應超過保證載荷的75%。M16螺栓的保證載荷為91.1 kN,在本實驗的預緊力作用下(靜態),螺紋聯接不會發生整體的塑性變形。此外,本研究所有實驗中螺紋聯接的各摩擦副均處于干摩擦狀態。
2 結果與分析
2.1 松動曲線的特征與擬合
圖2a與2b所示為不同實驗條件的橫向振動作用下螺紋聯接的松動曲線。由圖2a可見,夾緊力在松動初期經歷了快速衰減,之后進入緩慢的線形衰減階段。當振動次數足夠大時,螺栓疲勞斷裂。圖2b所示為前3 000個振動周期內夾緊力曲線在Y方向放大后的觀察結果,可見夾緊力呈現出波動式衰減,但整體上不是線性衰減。
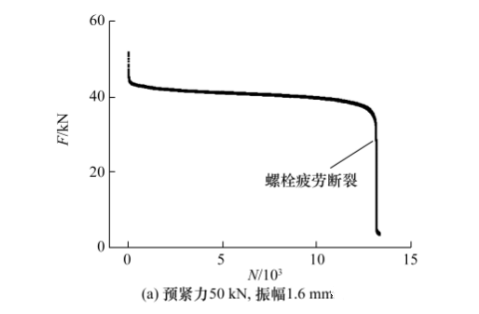
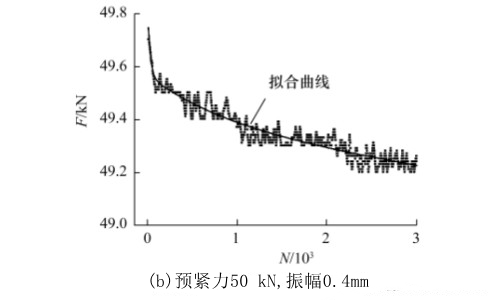
現有文獻對夾緊力線性衰減的機制已經有了深入的研究[16,?17],但對松動初期夾緊力非線性快速衰減的機制則較少關注。松動初期指的是夾緊力進入近似線性衰減階段之前的松動階段(如圖2a所示)。本研究采用數據處理軟件Origin對松動初期夾緊力變化的實驗數據進行了擬合分析。如圖2b所示,擬合分析表明在松動初期夾緊力的衰減可以用雙指數函數描述,
式中:?F表示夾緊力,N表示振動次數,A、?B、?D、?τ1、?τ2為模型函數的參數。式(1)表明松動初期存在兩個指數衰減過程:?A·e-N/τ1主導了圖2b中最初的幾個至幾十個振動周期內夾緊力的急速衰減,B·e-N/τ2主導了夾緊力在隨后的振動過程中相對緩慢的非線性衰減。?A·e-N/τ1與B·e-N/τ2可能分別反映了橫向振動作用下螺紋聯接的應變松弛過程與摩擦副的磨合(running-in)過程(將在第3節進一步討論)。
在式(1)中增加一個線性項就可以描述夾緊力在更長振動時間內的衰減過程,
2.2 振幅與預緊力對松動曲線特征的影響
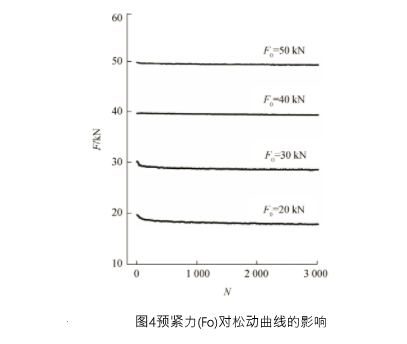
圖3以預緊力為50 kN的實驗結果為例,顯示了橫向振幅對松動曲線的影響。可見,振幅越大,夾緊力曲線波動越大,且夾緊力衰減越快。使用式(2)對圖3中各曲線進行擬合(擬合曲線見圖3),得到的模型函數各參數列于表1。由表1可以看出,參數A、?B、?C隨著振幅的增加而增加,亦即振幅越高,指數函數衰減的幅值越大且線性衰減的斜率越大;相應地,參數D隨著振幅的增加而減少。此外,從表1不能看出振幅對式(1)中指數衰減的時間常數τ1、?τ2的影響規律。
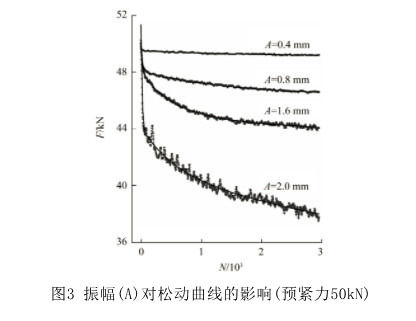
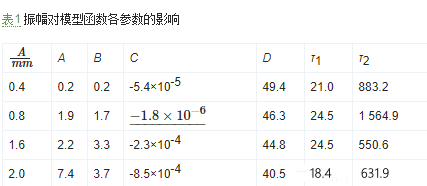
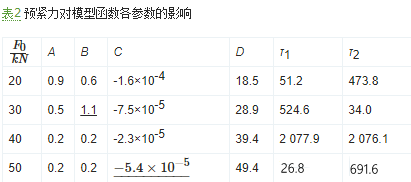
圖4以振幅為0.4 mm的實驗結果為例,顯示了預緊力對松動曲線的影響。可見,預緊力越小,松動初期夾緊力衰減的幅值越大。使用式(2)對圖4所示的松動曲線進行擬合分析,擬合得到的模型函數各參數列于表2。表2總體上反映出,預緊力越大,參數A、?B、?C的值越小。從表2不能看出預緊力對指數衰減的時間常數τ1、?τ2的影響規律。
參數A、?B、?C反映了松動初期夾緊力的衰減量及衰減速率。橫向振幅與預緊力對參數A、?B、?C的影響可以直觀地理解為:從橫向振動實驗的原理(圖1)來看,振幅越大,則施加在螺母上的橫向剪切力與松動力矩越大,因而夾緊力衰減越快;而預緊力越小,則螺紋聯接摩擦副的摩擦阻力越小,因而螺母更容易克服摩擦阻力發生松動方向的轉動。
表1與2中有個別數據點(以下劃線標明)與整體的趨勢不相符合,這反映了對松動曲線進行定量研究的困難。本研究比較了預緊力分別為50、 40、 30、 20 kN,振幅分別為0.4、 0.8、 1.2、 1.6、 2.0 mm 實驗條件下的松動曲線的擬合參數。總體而言,模型函數參數A、?B、?C的值隨振幅與預緊力的變化規律與上文所述是一致的;而時間常數τ1、?τ2的值隨振幅與預緊力的變化規律目前尚不清楚。
2.3 單個周期內夾緊力的變化
圖5所示為單個振動周期內夾緊力與橫向位移的同步變化關系。單個振動周期的起點定義為上連接板(圖1)位于原點并且向右運動的時刻。上連接板的位置由位移傳感器測得(如圖5b所示)。圖5c表明,在橫向振動實驗剛開始時夾緊力快速單調衰減(圖5c中第3、 4個周期所示)。第3個振動周期內,夾緊力減少量高達1 kN。經過最初的快速衰減之后,夾緊力在單個周期內隨著橫向位移的變化而交替增加或減少。在單個振動周期內夾緊力與橫向振動的位移之間沒有表現出恒定的相關性(如圖5c中第89、 90個周期所示)。
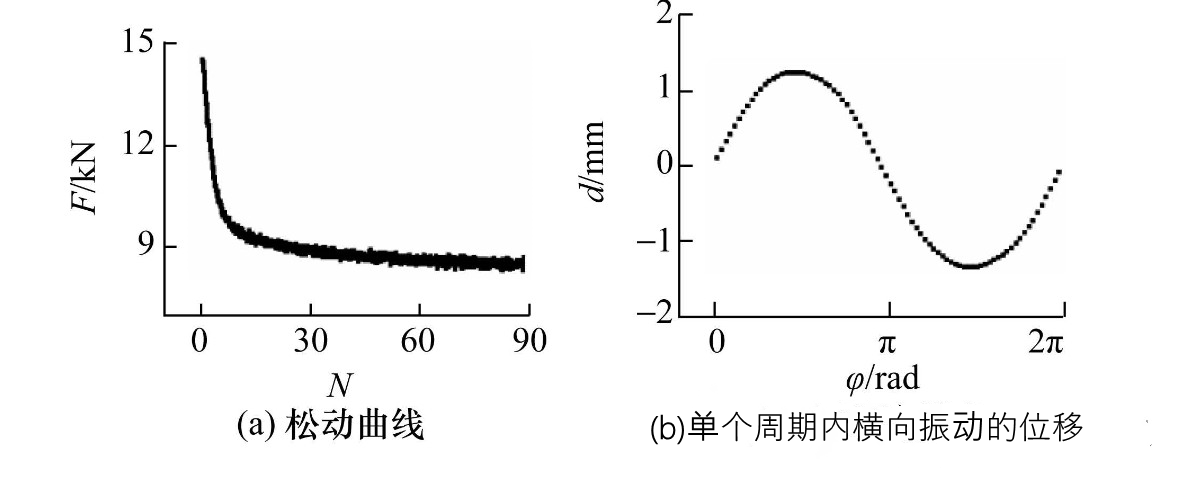
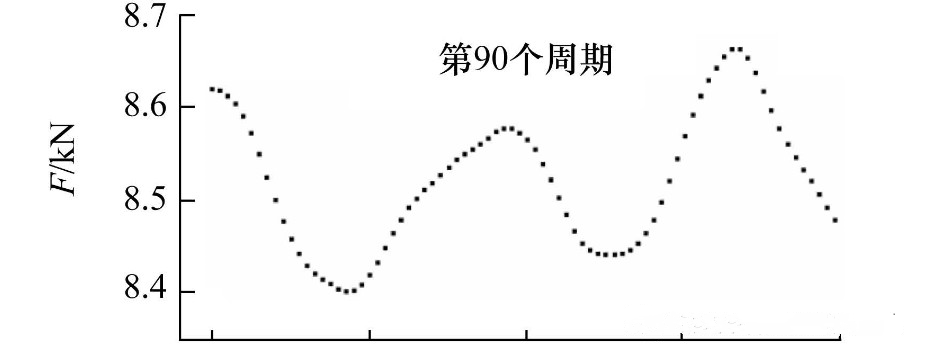
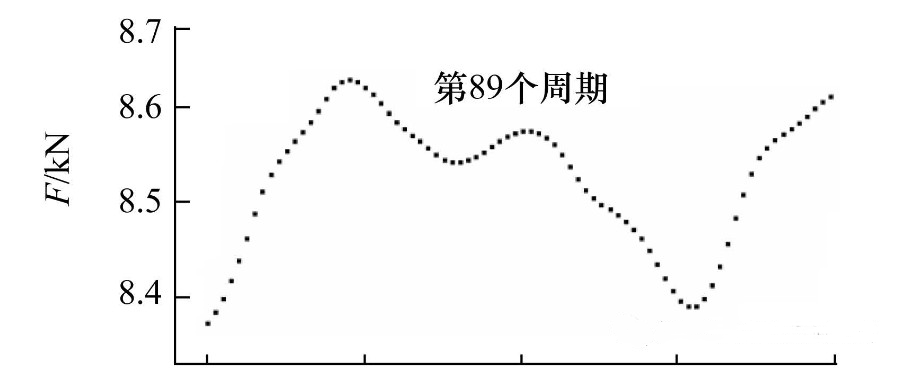
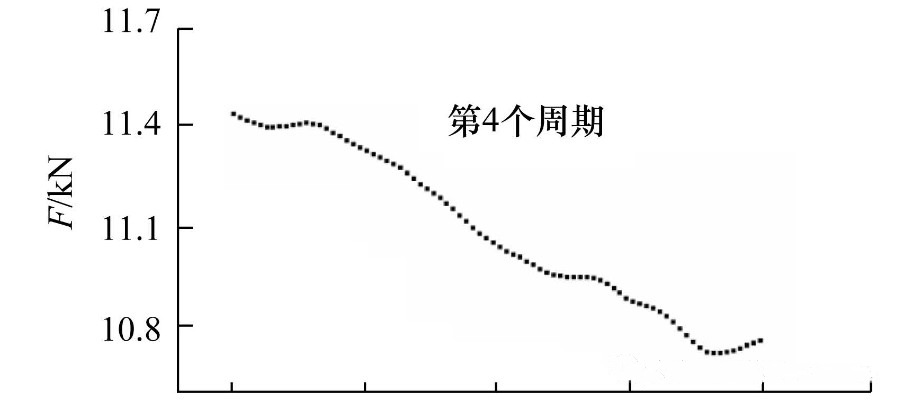
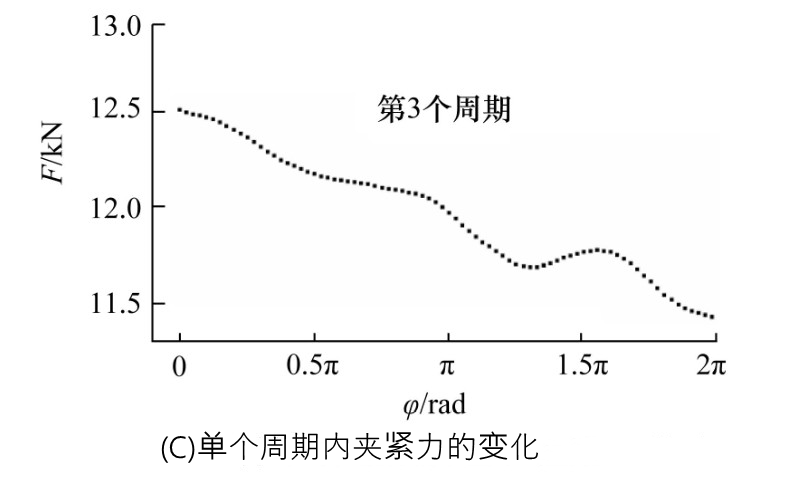
圖5?不同振動周期內夾緊力與振動角橫向位移(φ)的關系 (預緊力15 kN,振幅1.6 mm)
3 討 論3.1 夾緊力衰減函數的解讀
本研究表明,橫向振動作用下螺紋聯接的松動初期是一個呈指數衰減的過程。式(1)由兩個指數函數構成,是描述松動初期夾緊力變化的初步模型函數。指數函數A·e-N/τ1可能反映了螺栓與摩擦界面材料發生應變松弛所引起的快速松動。應變松弛會導致夾緊力的減少。施剛等[18]的研究表明,在靜態條件下,螺紋聯接擰緊后螺栓會發生應變松弛,在實驗初期,應變減小較快,而隨著時間增長,應變的減少越來越慢,最后趨于穩定。施剛等[18]觀察到的靜態條件下的應變松弛過程與本研究觀察到的橫向振動作用下夾緊力的衰減過程具有相似性。而且,橫向振動條件下,應變松弛不僅發生在受拉伸應力作用的螺栓上,也發生在受剪切應力作用的螺紋聯接摩擦副材料上。橫向振動提供的能量輸入能夠克服應變松弛的能壘,從而加速應變松弛的發生。
式(1)指數函數B·e-N/τ2可能反映了橫向振動作用下螺紋聯接摩擦副在松動初期的磨合過程。在磨合階段,螺紋聯接摩擦界面的粗糙峰發生交替的塑性變形,由于棘輪效應[14],塑性變形累積式增加,使得粗糙峰平坦化,從而導致摩擦系數變小。經過松動初期的磨合,摩擦系數才趨于穩定。如圖2b與圖3所示,夾緊力在松動初期呈波動式減少,這可能是由于在橫向振動引起的外加驅動力矩的作用下摩擦界面因摩擦系數減少而發生整體滑移,并導致夾緊力快速減少。為了驗證以上關于松動初期的磨合過程的假說,今后需要對螺紋聯接摩擦副在橫向振動過程中的摩擦系數進行動態測量。
從單個振動周期來看,夾緊力隨著橫向位移的變化而交替地增加或減少(圖5),這表明螺紋聯接在振動過程中發生了交替的擰緊與擰松過程。螺紋聯接在擰緊過程中,擰緊力矩T?f與夾緊力F之間滿足[3]

將式(3)與(4)相減可知,在相同的夾緊力下,總是有T?f>T?l。橫向振動作用下只要作用在螺母上的驅動力矩大于擰松力矩T?l,螺母在一個振動周期內擰松量必大于擰緊量,從而造成夾緊力的減少。這個機理已經被其他研究者所認識[4,?5,?6,?7]。式(3)與(4)只適用于靜態的擰緊與擰松過程,不能通過單個振動周期內外加力矩的變化推導出夾緊力的變化。
目前,鮮有研究關注單個周期內夾緊力隨位移的變化規律。Nassar與Housari[16,?17]假定橫向振動作用下螺紋聯接摩擦界面的摩擦系數恒定,推導出單個振動周期內施加于螺母上的力矩與橫向振動的位移之間存在恒定的關系。然而,圖5表明,單個振動周期內夾緊力與橫向位移之間沒有恒定的相關性。這可能說明單個振動周期內,由于螺紋聯接摩擦界面材料的粘彈性變形以及接觸狀況的動態變化,摩擦系數μ?t與μ?b并不是恒定值。
4 結 論
1) 橫向振動作用下螺紋聯接的松動過程可用雙指數函數來擬合:F=A?· e-N/τ1+B·e-N/τ2+C·N+D。式中:?F為夾緊力,N為振動次數,A、?B、?C、?D、?τ1、?τ2為模型函數的參數。式中的指數函數部分描述了松動初期夾緊力衰減的特點。
2) 橫向振動的振幅越大,模型函數的參數A、?B、?C的值越大;預緊力越小,參數A、?B、?C的值越大。振幅與預緊力對模型函數的時間常數τ1、?τ2的影響目前尚不清楚。


